Question

A random sample of the actual weight of 5-lb bags of mulch produces a mean of 4.963 lb and a standard deviation of 0.067 lb. If n=50, which of the following will give a 95% confidence interval for the mean weight (in pounds) of the mulch produced by this company?

A) 4.963±0.016.
B) 4.963±0.019.
C) 4.963±0.067.
D) 4.963±0.009.
E) None of the above.

Answer 1

the correct answer is B) 4.963±0.019.

Explanation:

Answer 2

Answer: B) 4.963±0.019.

Explanation:

Confidence interval for population mean ( when population standard deviation is not given) is given by :-

`\overline{x}\pm t^*(s)/(√(n))`

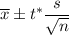
, where
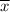`\overline{x}` = Sample mean

n= Sample size

s= sample standard deviation

t* = critical t-value.

As per given:

n= 50

Degree of freedom = n-1 =49

`\overline{x}= 4.963\ lb`

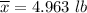
s= 0.067 lb

For df = 49 and significance level of 0.05 , the critical two-tailed t-value ( from t-distribution table) is 2.010.

Now , substitute all values in the formula , we get

`4.963\pm (2.010)(0.067)/(√(50))\\\\ 4.963\pm (2.010)(0.0094752)\\\\ 4.963\pm0.019045152\approx4.963\pm0.019`

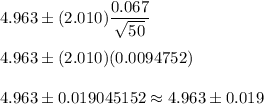
Hence, a 95% confidence interval for the mean weight (in pounds) of the mulch produced by this company is
`4.963\pm0.019`.

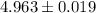Thus , the correct answer is B) 4.963±0.019.