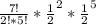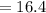Question

Suppose that two parents are both heterozygous for sickle cell anemia, which is an autosomal recessive disease. They have seven children. Use the binomial theorem to determine the probability that three of the children have sickle cell anemia and four of the children are healthy. Round your answer to the nearest hundredth.

Huntington\'s disease is an inherited autosomal dominant disorder that can affect both men and women. Imagine a couple has had seven children, and later in life, the husband develops Huntington\'s disease. He is tested and it is discovered he is heterozygous for the disease allele, Hh. The wife is also genetically tested for the Huntington\'s disease allele, and her test results show she is unaffected, hh. What is the percent probability that the first child of this couple will have Huntington\'s disease?also..

What is the probability that any two of the seven children will have Huntington\'s disease?

Answer 1

Part A

`0.108`

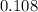
Part B

B.1

Fifty Percent

B.2

`16.4` %

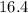Step-by-step explanation:

Part A

Given -

Both the parents are heterozygous for the sickle cell anemia

Let the genotype of the parents be

Ss

where S is the allele for presence of sickle cell anemia

and s is the allele absence of sickle cell anemia

If the above two parents are crossed, following offspring are produced

Ss * Ss

SS, Ss, Ss, ss

The probability of children with sickle cell anemia is equal to

`(3)/(4)`

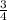
The probability of children with sickle cell anemia is equal to

`(1)/(4)`

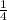
Probability that three of the children have sickle cell anemia and four of the children are healthy

`(7!)/(3! * 4!) * (3)/(4)^4 * (1)/(4)^3\\ = 35 * (81)/(256 *64) \\= 0.108`

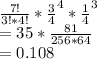
Part B

B.1

Hh * hh

Hh, Hh, hh, hh

The first child of the parent has a probability of fifty percent to have Huntington\'s disease

B.2

`(7!)/(2!*5!) * (1)/(2)^2 * (1)/(2)^5`

`= 16.4`