Question

A department store is holding a drawing to give away free shopping sprees. There are customers who have entered the drawing: live in the town of Gaston, live in Pike, and live in Wells. Two winners will be selected at random. What is the probability that both winners live in Wells?

Answer 1

The probability of selecting two winners from Wells is,
`(z(z-1))/((x+y+z)(x+y+z-1))`

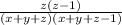
Explanation:

Let us assume that x people entered the drawing were from Gaston, y people entered the drawing were from Pike and z people entered the drawing were from Wells.

Total number of people who entered the drawing is, N = x + y + z.

It is provided that 2 winners are selected at random.

The event of selecting the first and second winner are not related, i.e. they are independent.

Then the first winner can be selected from Wells in z ways.

And the second winner can be selected, also from Wells in (z - 1) ways.

The probability of selecting both the winners from Wells is:

`P(Both\ the\ winners\ were\ from\ Wells)=(z)/(x+y+x)* (z-1)/(x+y+z-1) =(z(z-1))/((x+y+z)(x+y+z-1))`

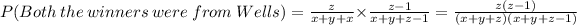
Thus, the probability of selecting two winners from Wells is,
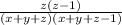`(z(z-1))/((x+y+z)(x+y+z-1))`.