Answer:
(a) 2 feet.
(b) 2 feet.
Explanation:
We have been given that the velocity function
 in feet per second, is given for a particle moving along a straight line.
in feet per second, is given for a particle moving along a straight line.
(a) We are asked to find the displacement over the interval
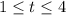 .
.
Since velocity is derivative of position function , so to find the displacement (position shift) from the velocity function, we need to integrate the velocity function.

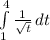
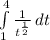
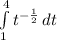
Using power rule, we will get:
![\left[\frac{t^{-(1)/(2)+1}}{-(1)/(2)+1}}\right] ^4_1](https://img.qammunity.org/2021/formulas/mathematics/high-school/rraa37po11lcqhxz18jsb6r0636r9pw9or.png)
![\left[\frac{t^{(1)/(2)}}{(1)/(2)}}\right] ^4_1](https://img.qammunity.org/2021/formulas/mathematics/high-school/7u25557b6ob6ryfbm96d04t2h325kvcg9z.png)
![\left[2t^{(1)/(2)}\right] ^4_1](https://img.qammunity.org/2021/formulas/mathematics/high-school/f9wu00iayjd77gevv0rdrv31j5bbylc94d.png)
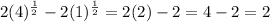
Therefore, the total displacement on the interval
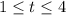 would be 2 feet.
would be 2 feet.
(b). For distance we need to integrate the absolute value of the velocity function.
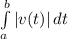
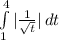
Since square root is not defined for negative numbers, so our integral would be
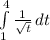 .
.
We already figured out that the value of
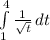 is 2 feet, therefore, the total distance over the interval
is 2 feet, therefore, the total distance over the interval
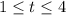 would be 2 feet.
would be 2 feet.