Question

The mass of the Sun is 2 × 1030 kg, the mass of the Earth is 6 × 1024 kg, and their center-to-center distance is 1.5 × 1011 m. Suppose that at some instant the Sun's momentum is zero (it's at rest). Ignoring all effects but that of the Earth, what will the Sun's speed be after 3 days? (Very small changes in the velocity of a star can be detected using the "Doppler" effect, a change in the frequency of the starlight, which has made it possible to identify the presence of planets in orbit around a star.)

Answer 1

0.00461031264 m/s

Step-by-step explanation:

G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²

M = Mass of the Earth = 6 × 10²⁴ kg

r = Distance between Earth and Sun =
`1.5* 10^(11)\ m`

t = Time taken = 3 days

Acceleration is given by

`a=(GM)/(r^2)\\\Rightarrow a=(6.67* 10^(-11)* 6* 10^(24))/((1.5* 10^(11))^2)\\\Rightarrow a=1.77867* 10^(-8)\ m/s^2`

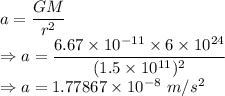
Velocity of the star

`v=u+at\\\Rightarrow v=0+1.77867* 10^(-8)* 3* 24* 60* 60\\\Rightarrow v=0.00461031264\ m/s`

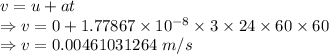
The Sun's speed will be 0.00461031264 m/s