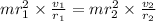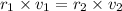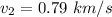Question

Halley's comet moves about the Sun in an elliptical orbit, with its closest approach to the Sun being 0.59 A.U. and its greatest distance being 35 A.U. (A.U. is the Earth-Sun distance). If the comet's speed at closest approach is 47 km/s, what is its speed when it is farthest from the Sun?

Answer 1

Step-by-step explanation:

Given

Halley's closest distance from sun is
`r_1=0.59\ A.U.`

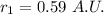
Greatest distance is
`r_2=35\ A.U.`

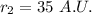
Comet's speed at closest approach is
`v_1=47\ km/s`

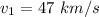
As there is no external torque so angular momentum of comet about the sun is conserved

`L_1=L_2`

`mr_1^2* \omega _1=mr_2^2* \omega _2`

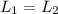
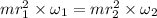
where
`\omega =angular\ velocity`

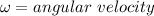
This can be written as
`\omega =(v)/(r)`

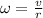
Therefore

`mr_1^2* (v_1)/(r_1)=mr_2^2* (v_2)/(r_2)`

`r_1* v_1=r_2* v_2`

`0.59* 47=35* v_2`

`v_2=0.79\ km/s`