The value of
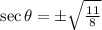 .
.
Solution:
Given data:
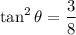
To find the value of
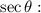
Using trigonometric identity,
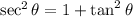
Substitute
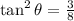 in the identity, we get
in the identity, we get

1 can be written as
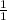 .
.
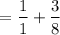
Do cross multiplication.

Denominators are same, so you can add the fractions.

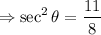
Taking square root on both sides, we get
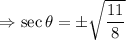
Option B is the correct answer.
Hence the value of
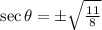 .
.