Question

What is the average rate of change for ƒ(x) = −4x + 40 over the interval 1 ≤ x ≤ 3?

Answer 1

−30

Explanation:

−30 is the average rate of change for ƒ(x) = −4x + 40 over the interval 1 ≤ x ≤ 3.

ƒ(b) − ƒ(a)

b − a

= ƒ(3) − ƒ(1)

3 − 1

= −24 − 36

2

= −60

2

= −30

Answer 2

The average rate of change is = - 4

Explanation:

If y = f(x) is a function then the average rate of change for f(x) between the interval a ≤ x ≤ b is given by

`(f(b) - f(a))/(b - a)`.

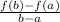Now, in this case the function is given by f(x) = - 4x + 40 and the interval is 1 ≤ x ≤ 3.

Therefore, f(1) = - 4(1) + 40 = 36 and f(3) = - 4(3) + 40 = 28

So, the average rate of change is =
`(28 - 36)/(3 - 1) = - (8)/(2) = - 4` (Answer)