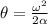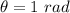Answer:
Step-by-step explanation:
Given
magnitude of centripetal acceleration is twice the magnitude of tangential acceleration
Suppose
 is theta angle rotated by electric drill
is theta angle rotated by electric drill
it is given that it starts from rest i.e.
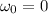
suppose
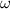 and
and
 is the final angular velocity and angular acceleration
is the final angular velocity and angular acceleration
using rotational motion equation
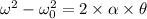
where
 =angle turned by drill
=angle turned by drill
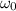 =initial angular velocity
=initial angular velocity
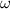 =final angular velocity
=final angular velocity
 =angular acceleration
=angular acceleration
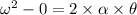
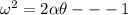
It is also given that centripetal acceleration is twice the magnitude of tangential i.e.
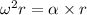
where r=radial distance of any point from axis of drill
i.e.
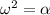
substitute this value to equation 1
we get