Question

A nonconducting sphere has radius R = 2.36 cm and uniformly distributed charge q = +2.50 fC. Take the electric potential at the sphere's center to be V0 = 0. What is V at radial distance r = 1.45 cm?

Answer 1

Step-by-step explanation:

It is known that inside a sphere with uniform volume charge density the field will be radial and has a magnitude E that can be expressed as follows.

E =
`(q)/(4 \p \epsilon_(o)R^(3))r`

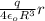
V =
`-\int_(0)^(r)E. dr`

=
`-\int_(0)^(r)(q)/(4 \p \epsilon_(o)R^(3))r dr`

=
`((q)/(4 \p \epsilon_(o)R^(3)))((r^(2))/(2))`

=
`(-qr^(2))/(8 \pi \epsilon_(o)R^(3))`

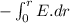
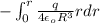
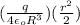
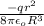
At r = 1.45 cm =
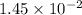`1.45 * 10^(-2)` (as 1 m = 100 cm)

V =
`(2.50 * 10^(-15) * 1.45 * 10^(-2))/(8 * 3.1416 * 8.85 * 10^(-12) * 2.36 * 10^(-2))`

=
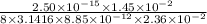
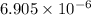`6.905 * 10^(-6)` mV

Thus, we can conclude that value of V at radial distance r = 1.45 cm is
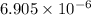`6.905 * 10^(-6)` mV.