Question

A private opinion poll is conducted for a politician to determine what proportion of the population favors adding more national parks. How large a sample is needed in order to be 98 ​% confident that the sample proportion will not differ from the true proportion by more than 6 ​%?

Answer 1

n≅376

So sample size is 376.

Explanation:

The formula we are going to use is:

`n=pq((z_(\alpha/2))/(E))^(2)`

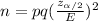
where:

n is the sample size

p is the probability of favor

q is the probability of not in favor

E is the Margin of error

z is the distribution

α=1-0.98=0.02

α/2=0.01

From cumulative standard Normal Distribution

`z_(\alpha/2)=2.326`

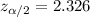
p is taken 0.5 for least biased estimate, q=1-p=0.5

`n=0.5*0.5((2.326)/(0.06))^(2)\\n=375.71`

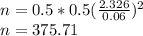
n≅376

So sample size is 376