Question

Ethan decides to type up some documents while waiting for the meeting to start he can type two pages every 1/8 hour if the meeting starts 3/4 hour later than the scheduled time how many pages can he typed before the meeting starts

Answer 1

Ethan can type 12 pages before the meeting starts.

Explanation:

Given:

Number of pages he can type =2

Number of hours he can type 2 pages =
`\frac{1}8\ hrs`

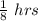
We need to find number of pages he can type in
`\frac34\ hrs`

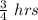
Solution:

Now first we will find number of pages in 1 hour

So we can say;

In
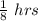`\frac{1}8\ hrs` = 2 pages

In 1 hour = number of pages he can type in 1 hour

By Using Unitary method we get;

number of pages he can type in 1 hour =
`(2)/(\frac18) =(2*8)/(1)=16\ pages`

Now we can say that;

In 1 hour = 16 pages

So
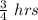`\frac34\ hrs` = number of pages he can type in
`\frac34\ hrs`

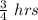
Again By using Unitary method we get;

number of pages he can type in
`\frac34\ hrs` =
`16* \frac34 = 12\ pages`

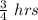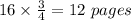
Hence Ethan can type 12 pages before the meeting starts.