Question

which choice is the explicit formula for the following geometric sequence? 0.3, -0.06, 0.012, -0.0024, 0.00048

Answer 1

a n+0.3(-0.2)n-1

Explanation:

Answer 2

`a_(n) = 0.3(- 0.2)^(n - 1)`

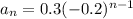
Explanation:

The given sequence is 0.3, - 0.06, 0.012, - 0.0024, 0.00048 ........ so on.

Now, this is a G.P. sequence with common ratio
`(- 0.06)/(0.3) = - 0.2`.

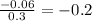Now, the explicit formula of the given series will be

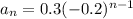`a_(n) = 0.3(- 0.2)^(n - 1)` , where
`a_(n)` is the nth term of the G.P. sequence.

Now, for n = 1,
`a_(1) = 0.3(- 0.2)^(1 - 1) = 0.3`.

For, n = 2,
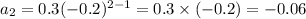`a_(2) = 0.3(- 0.2)^(2 - 1) = 0.3 * (- 0.2) = - 0.06` and so on. (Answer)