Question

Rebecca and dan are biking in a national park for three days they rode 5 3/4 hours the first day and 6 4/5 hours the second day how long do they need to ride on the third day to make their goal of biking a total of 20 hours in the park

Answer 1

Rebecca and Dan need to ride
`7(9)/(20)\ hrs.` on the third day in order to achieve goal of biking.

Explanation:

Given:

Goal of Total number of hours of biking in park =20 hours.

Number of hours rode on first day =
`5\frac34 \ hrs.`

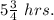
So we will convert mixed fraction into Improper fraction.

Now we can say that;

To Convert mixed fraction into Improper fraction multiply the whole number part by the fraction's denominator and then add that to the numerator,then write the result on top of the denominator.

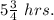`5\frac34 \ hrs.` can be Rewritten as
`(23)/(4)\ hrs`

Number of hours rode on first day =
`(23)/(4)\ hrs`

Also Given:

Number of hours rode on second day =
`6\frac45 \ hrs`

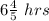
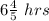`6\frac45 \ hrs` can be Rewritten as
`(34)/(5)\ hrs.`

Number of hours rode on second day =
`(34)/(5)\ hrs.`

We need to find Number of hours she need to ride on third day in order to achieve the goal.

Solution:

Now we can say that;

Number of hours she need to ride on third day can be calculated by subtracting Number of hours rode on first day and Number of hours rode on second day from the Goal of Total number of hours of biking in park.

framing in equation form we get;

Number of hours she need to ride on third day =
`20-(23)/(4)-(34)/(5)`

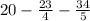
Now we will use LCM to make the denominators common we get;

Number of hours she need to ride on third day =
`(20*20)/(20)-(23*5)/(4*5)-(34*4)/(5*4)= (400)/(20)-(115)/(20)-(136)/(20)`

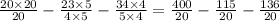
Now denominators are common so we will solve the numerator we get;

Number of hours she need to ride on third day =
`(400-115-136)/(20)=(149)/(20)\ hrs \ \ Or \ \ 7(9)/(20)\ hrs.`

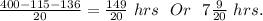
Hence Rebecca and Dan need to ride
`7(9)/(20)\ hrs.` on the third day in order to achieve goal of biking.