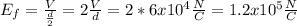Answer:
Step-by-step explanation:
For this case we know that the electric field is given by:
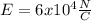
And we want to find the final electric field assuming that the separation is halved and becomes d/2.
For this case we can use the following two equations:
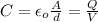 (1)
(1)
 (2)
(2)
Where Q represent the charge, V the voltage, d the distance, A the area.
We can rewrite the equation (2) like this:
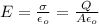 (3)
(3)
And we can solve for Q from equation (1)like this:
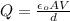
And if we replace into equation (3) the previous result we got:
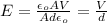
And since the the electric field not change and the distance would be the half we have that the final electric field would be given by: