Answer:
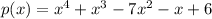
Explanation:
The polynomial function has zeros
x=1, x=2,x=-3,x=-1
This means the factored form of the polynomial is
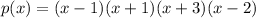
We expand to get:
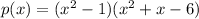
We expand further to get:
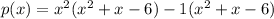
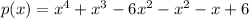
This simplifies to:
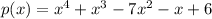
This is the standard form of the polynomial since it is written in descending powers of x.