Question

What is the missing reason in the proof?

Given: ∠ABC is a right angle, ∠DBC is a straight angle
Prove: ∠ABC ≅ ∠ABD

A horizontal line has points D, B, C. A line extends vertically from point B to point A. Angle A B C is a right angle.

A 2-column table has 8 rows. The first column is labeled Statements with entries angle A B C is a right angle, angle D B C is a straight angle, m angle A B C = 90 degrees, m angle D B C = 180 degrees, m angle A B D + m angle A B C = m angle D B C, m angle A B D + 90 degrees = 180 degrees, m angle A B D = 90 degrees, angle A B C is-congruent-to angle A B D. The second column is labeled Reasons with entries, given, given, definition of right angle, definition of straight angle, angle addition property, substitution property, subtraction property, and question mark.

definition of angle bisector
segment addition property
definition of congruent angles
transitive property

Answer 1

C. definition of congruent angles.

Explanation: This is the correct answer on Edge 2021, just took the unit test. Hope this helps ^-^.

Answer 2

Third option: Definition of Congruent angles.

Explanation:

For this exercise it is important to know the definition Congruent angles.

Congruent angles are defined as those angles that have equal measure.

The symbol used for Congruent angles is the following:

≅

Keep the explanation above on mind.

In this case, you know that
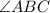`\angle ABC` measures 90 degrees (This is also known as "Rigth angle"):

`\angle ABC=90\°`

And you can observe in the table attached that the measure of
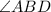`\angle ABD` is also 90 degrres:

`\angle ABD=90\°`

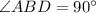
Therefore, since they have exactly the same measure, these angles are congruent. Then:

`\angle ABC` ≅
`\angle ABD`

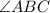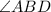
Based on this, you can identify that the missing reason number 8 is: Definition of Congruent angles.