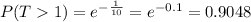Question

The time between breakdowns of an alarm system is exponentially distributed with mean 10 days. What is the probability that there are no breakdowns on a given day?

Answer 1

`P(T>1) = e^{-(1)/(10)}= e^(-0.1)= 0.9048`

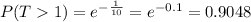
Explanation:

Previous concepts

The exponential distribution is "the probability distribution of the time between events in a Poisson process (a process in which events occur continuously and independently at a constant average rate). It is a particular case of the gamma distribution". The probability density function is given by:

`P(X=x)=\lambda e^(-\lambda x)`

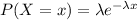
Solution to the problem

For this case the time between breakdowns representing our random variable T is exponentially distirbuted
`T \sim Exp (\mu = 10)`

So on this case we can find the value of
`\lambda` like this:

`\lambda = (1)/(\mu) = (1)/(10)`

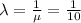
So then our density function would be given by:

`P(T)=\lambda e^{-(t)/(10)}`

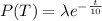
The exponential distribution is useful when we want to describe the waiting time between Poisson occurrences. If we assume that the random variable T represent the waiting time between two consecutive event, we can define the probability that 0 events occurs between the start and a time t, like this:

`P(T>t)= e^(-\lambda t)`

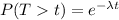
And on this case we are looking for this probability:

`P(T>1) = e^{-(1)/(10)}= e^(-0.1)= 0.9048`