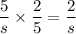Answer:
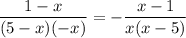
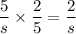
Explanation:
Errors in Algebraic Operations
It's usual that students make mistakes when misunderstanding the application of algebra's basic rules. Here we have two of them
- When we change the signs of all the terms of a polynomial, the expression must be preceded by a negative sign
- When multiplying negative and positive quantities, if the number of negatives is odd, the result is negative. If the number of negatives is even, the result is positive.
- Not to confuse product of fractions with the sum of fractions. Rules are quite different
The first expression is
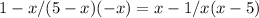
Let's arrange into format:
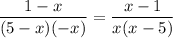
We can clearly see in all of the factors in the expression the signs were changed correctly, but the result should have been preceeded with a negative sign, because it makes 3 (odd number) negatives, resulting in a negative expression. The correct form is
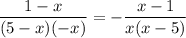
Now for the second expression
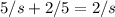
Let's arrange into format
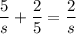
It's a clear mistake because it was asssumed a product of fractions instead of a SUM of fractions. If the result was correct, then the expression should have been