To solve this problem we will apply the concepts related to centripetal acceleration, which will be the same - by balance - to the force of gravity on the body. To find this acceleration we must first find the orbital velocity through the Doppler formulas for the given periodic signals. In this way:
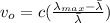
Here,
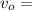 Orbital Velocity
Orbital Velocity
 Maximal Wavelength
Maximal Wavelength
 Average Wavelength
Average Wavelength
c = Speed of light
Replacing with our values we have that,
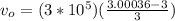
Note that the average signal is 3.000000m
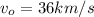
Now using the definition about centripetal acceleration we have,
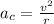
Here,
v = Orbit Velocity
r = Radius of Orbit
Replacing with our values,
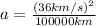
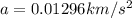
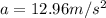
Applying Newton's equation for acceleration due to gravity,
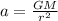
Here,
G = Universal gravitational constant
M = Mass of the planet
r = Orbit
The acceleration due to gravity is the same as the previous centripetal acceleration by equilibrium, then rearranging to find the mass we have,

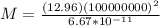
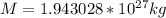
Therefore the mass of the planet is
