Question

If the work required to stretch a spring 2 ft beyond its natural length is 6 ft-lb, how much work is needed to stretch it 6 in. beyond its natural length?

Answer 1

0.375 feet-lb

Explanation:

We have been given that the work required to stretch a spring 2 ft beyond its natural length is 6 ft-lb. We are asked to find the work needed to stretch the spring 6 in. beyond its natural length.

We can represent our given information as:

`6=\int\limits^2_0 {F(x)} \, dx`

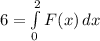
We will use Hooke's Law to solve our given problem.

`F(x)=kx`

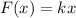
Substituting this value in our integral, we will get:

`6=\int\limits^2_0 {kx} \, dx`

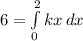
Using power rule, we will get:

`6=\left[ (kx^2)/(2) \right ]^2_0`

`6=(k(2)^2)/(2)-(k(0)^2)/(2)`

`6=(4k)/(2)-0\\\\k=3`

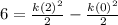
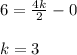
We know that 6 inches is equal to 0.5 feet.

Work needed to stretch it beyond 6 inches beyond its natural length would be
`\int\limits^(0.5)_0 {kx} \, dx =\int\limits^(0.5)_0 {3x} \, dx`

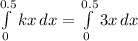
Using power rule, we will get:

`\int\limits^(0.5)_0 {3x} \, dx = \left [(3x^2)/(2)\right]^(0.5)_0`

`(3(0.5)^2)/(2)-(3(0)^2)/(2)\Rightarrow (3(0.25))/(2)-0=(0.75)/(2)=0.375`

Therefore, 0.375 feet-lb work is needed to stretch it 6 in. beyond its natural length.