Question

If you bet $1 that a sum of 5 will turn up, what should the house pay (plus returning your $1 bet) if a sum of 5 turns up in order for the game to be fair?

Answer 1

Here is the complete question.

1). What are the odds for rolling a sum of 5 in a single roll of two fair dice?

2). If you bet $1 that a sum of 5 will turn up, what should the house pay (plus returning your $1 bet) if a sum of 5 turns up in order for the game to be fair?

Answer:

1).
`(1)/(8)`

2). $8.

Explanation:

1).

The sample space (S) for rolling two fair dice is given as the following parameters illustrated below:

Let F represent the event that the sum of both dice turns up is 5.

F = [(1,4),(2,3),(3,2),(4,1)}

∴ The probability for an event F is illustrated below as:

`(P(F))/(P(F'))`
`=((4)/(36) )/(1-(4)/(36) )`

`=((4)/(36) )/((32)/(36) )`

`={(4)/(36)}*(36)/(32)`

=
`(1)/(8)`

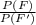
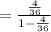
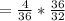
2). From above, we can see that the probability for rolling a sum of 5 are 1 to 8. Therefore, if you roll a sum of 5, in order for the game to be fair, the house is required to pay $8.