Answer:
Math will take over Ana's brain at 4.4 hours
Explanation:
Exponential Grow
The population of the nanobots follows the equation
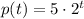
We must find the value of t such that the population of nanobots is 106 or more, that is

We'll solve the equation
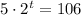
Dividing by 5
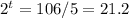
Taking logarithms
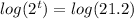
By logarithms property

Solving for t
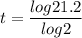
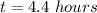
Math will take over Ana's brain at 4.4 hours