Question

Find the probability of having 2, 3, or 4 successes in five trials of a binomial experiment in which the probability of success is 40%.

Round to the nearest tenth of a percent
[?]%

Answer 1

P=65%

Explanation:

Binomial Distribution

The probability will be calculated by using the Binomial Distribution with n independent events each with a probability of success equal to p with k successes.

The PMF (Probability Mass Function) is

`\displaystyle F(k,n,p)=\binom{n}{k}p^kq^(n-k)`

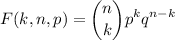
Where

`q = 1-p`

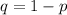
We have n=5trials with k=2, 3, or 4 successes. Each individual experience has
`p = 0.4 , q = 0.6`

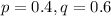
First, we compute for k=2

`\displaystyle F(2,5,0.4)=\binom{5}{2}0.4^20.6^(3)=0.3456`

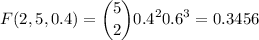
Now for k=3

`\displaystyle F(3,5,0.4)=\binom{5}{3}0.4^30.6^(2)=0.2304`

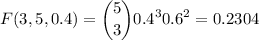
Finally for k=4

`\displaystyle F(4,5,0.4)=\binom{5}{4}0.4^40.6^(1)=0.0768`

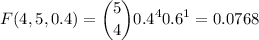
The required probability is

`P=0.3456+0.2304+0.0768=0.6528`

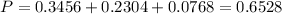
P=65%