Answer:
⠀
Explanation:
⠀
As it is given that, the length of a rectangle is 5 in longer than its width and the perimeter of the rectangle is 58 in and we are to find the length and width of the rectangle. So,
⠀
Let us assume the width of the rectangle as x inches and therefore, the length will be (x + 5) inches .
⠀
Now, According to the Question :
⠀

⠀
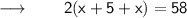
⠀
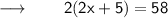
⠀
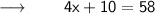
⠀
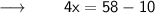
⠀
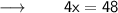
⠀
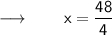
⠀

⠀
Therefore,
- The width of the rectangle is 12 inches .
⠀
Now, We are to find the length of the rectangle:
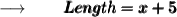
⠀

⠀

⠀
Therefore,
- The length of the rectangle is 17 inches .
⠀