Question

ABCD is a parallelogram. Segment AC = 4x + 10. Find the value of x and y.

Answer 1

The values of x and y in the diagonals of the parallelogram are x=0 and y=5

Explanation:

Given that ABCD is a parallelogram

And segment AC=4x+10

From the figure we have the diagonals AC=3x+y and BD=2x+y

By the property of parallelogram the diagonals are congruent

∴ we can equate the diagonals AC=BD

That is 3x+y=2x+y

3x+y-(2x+y)=2x+y-(2x+y)

3x+y-2x-y=2x+y-2x-y

x+0=0 ( by adding the like terms )

∴ x=0

Given that segment AC=4x+10

Substitute x=0 we have AC=4(0)+10

=0+10

=10

∴ AC=10

Now (3x+y)+(2x+y)=10

5x+2y=10

Substitute x=0, 5(0)+2y=10

2y=10

`y=(10)/(2)`

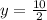
∴ y=5

∴ the values of x and y are x=0 and y=5