19 small mowers and 11 large mowers are sold
Solution:
Let "a" be the number of small mowers sold
Let "b" be the number of large mowers sold
Cost of each small mower = $ 249.99
Cost of each large mower = $ 329.99
30 total mowers were sold
Therefore,
a + b = 30
a = 30 - b ------------- eqn 1
The total sales for a given year was $8379.70
Thus we frame a equation as:
number of small mowers sold x Cost of each small mower + number of large mowers sold x Cost of each large mower = 8379.70
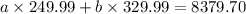
249.99a + 329.99b = 8379.70 ---------- eqn 2
Let us solve eqn 1 and eqn 2
Substitute eqn 1 in eqn 2
249.99(30 - b) + 329.99b = 8379.70
7499.7 - 249.99b + 329.99b = 8379.70
80b = 8379.70 - 7499.7
80b = 880
Divide both sides by 80
b = 11
Substitute b = 11 in eqn 1
a = 30 - 11
a = 19
Thus 19 small mowers and 11 large mowers are sold