Question

The width of a rectangular painting is 3in. More than twice the height. A frame that is 2.5 in. Wide goes around the painting

Answer 1

Question:

A width of a rectangular painting is 3 in. More than twice the height. A frame that is 2.5 in. Wide goes around the painting

a. write an expression for the combined area of the painting and frame.

b. use the expression to find the combined area when the height of the painting is 12 in.

c. use the expression to find the combined area when the height of the the painting is 15 in.

Answer:

a) (h + 5)(2h + 8) is the expression for the combined area of the painting and frame

b) The combined area when h = 12 is 544 square inches

c) The combined area when h = 15 is 760 square inches

Solution:

Given that,

A frame that is 2.5 inches wide goes around the painting

The frame will go around all 4 sides of the painting.

That means that the length of each side of the painting will increase by 2.5 inches

Therefore,

The height of painting and frame is:

h = h + 2.5 + 2.5

h = h + 5

(2.5 inches on the top and the bottom)

Also given that,

Width of a rectangular painting is 3 inches more than twice the height

w = 3 + 2h

Now the width of painting and frame is:

w = 3 + 2h + 2.5 + 2.5

(Again, 2.5 inches on the top and the bottom)

w = 2h + 8

Thus the combined area of the painting and frame is:

`Combined\ area = (h+5)(2h+8)`

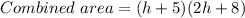
B) Substitute h = 12 inches

`Combined\ area = (12+5)(2(12)+8)\\\\Combined\ area = 17 * (24+8) = 17 * 32\\\\Combined\ area = 544`

Thus the combined area when h = 12 is 544 square inches

C) Substitute h = 15 inches

`Combined\ area = (15+5)(2(15)+8)\\\\Combined\ area = 20 * (30+8) = 20 * 38\\\\Combined\ area = 760`

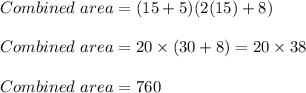
Thus combined area when h = 15 is 760 square inches