Question

If you have 108 inches of wood to make a picture fram what is the greatest area if a = -w2 + 54w

Answer 1

The greatest area possible is 729
`inch^(2)`

Explanation:

i) If a =
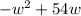`-w^(2) + 54w` where w is the width of the picture frame

differentiating on both sides we get

`(da)/(dw) = -2w + 54`

Differentiating the above again on both sides we get
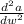`(d^2a)/(dw^2)` = -2

Since the second order derivative is negative then we can get the solution for the maximum area by equating the fist order derivative equation to 0.

Therefore -2w + 54 = 0 therefore w = 27.

ii) If we substitute w = 27 into the equation in ii) we get

a =
`-(27)^2 +(54* 27)` = (54 - 27)
`*`(27) =
`27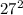^(2)` = 729