Question

A square is 3 inches on each side. A small square, x inches on each side, is cut out from each corner of the original square. Represent the area of the remaining portion of the square in the form of a polynomial function A(x)

Answer 1

`A(x) = 91-4x^2`

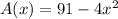
Explanation:

We are given the following in the question:

A square is 3 inches on each side. A small square, x inches on each side, is cut out from each corner of the original square.

The attached image shows the obtained square.

Area of square =

`s^2`

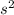
where s is the side of the square.

Area of bigger square =

`(9)^2 = 81\text{ square inches}`

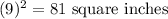
Area of smaller square =
`x^2`

Area of remaining portion =

Area of bigger square - 4(Area of smaller square)

`A(x) = 91-4x^2`

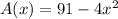
is the required polynomial function that gives remaining portion of the square.