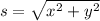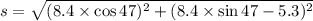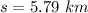Question

An explorer is caught in a whiteout (in which the snowfall is so thick that the ground cannot be distinguished from the sky) while returning to base camp. He was supposed to travel due north for 5.3 km, but when the snow clears, he discovers that he actually traveled 8.4 km at 47o north of due east. (a) How far and (b) in what direction (south of due west) must he now travel to reach base camp

Answer 1

`s=5.79\ km`

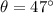`\theta=47^(\circ)` east of south

Step-by-step explanation:

Given:

• distance of the person form the initial position,
  `d'=8.4\ km`

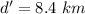
• direction of the person from the initial position,
  `47^(\circ)` north of east

• distance supposed to travel form the initial position,
  `d=5.3\ km`

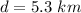
• direction supposed to travel from the initial position, due North

Now refer the schematic for visualization of situation:

`y=d'.\sin47^(\circ)-d`

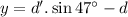
`y=8.4* \sin47-5.3` ...............(1)

`x=d'.\cos47^(\circ)`

`x=8.4* \cos47^(\circ)` .................(2)

Now the direction of the desired position with respect to south:

`\tan\theta=(y)/(x)`

`\tan\theta=(8.4* \sin47)/(8.4* \cos47)`

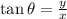
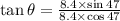
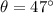`\theta=47^(\circ)` east of south

Now the distance from the current position to the desired position:

`s=√(x^2+y^2)`

`s=√((8.4* \cos47)^2+(8.4* \sin47-5.3)^2)`

`s=5.79\ km`