Question

The time needed to complete a final examination in a particular college course is normally distributed with a mean of 80 minutes and a standard deviation of 10 minutes. Answer the following questions:

A) What is the probability of completing the exam in ONE hour or less?

B) what is the probability that a student will complete the exam in more than 60 minutes but less than 75 minutes?

C) Assume that the class has 60 students and that the examination period is 90 minutes in length. How many students do you expect will be unable to compete the exam in the allotted time?

Answer 1

Part A:

Probability is P(z<-2)=1-0.9772=0.0228

Part B:

P(-2<z<-0.5)=0.2857

Part C:

Number of students unable to complete the exam=60-50=10 students

Explanation:

Part A:

Mean=μ=80 min

Standard Deviation=σ=10 min

Formula:

`z=(\bar x- \mu)/(\sigma)`

where:

`\bar x=60\ min`

`z=(60-80)/(10)\\ z=-2`

Probability is P(z<-2)

From the probability distribution tables (Cumulative Standardized normal distribution table)

Probability is P(z<-2)=1-0.9772=0.0228

Part B:

For 75 min:

`z=(75-80)/(10)\\ z=-0.5`

For
`\bar x=60\ min`

`z=(60-80)/(10)\\ z=-2`

From the probability distribution tables (Cumulative Standardized normal distribution table)

P(-2<z<-0.5)=P(z<-0.5)-P(z<-2)

P(-2<z<-0.5)=(1-0.6915)-(1-0.9772)

P(-2<z<-0.5)=0.2857

Part C:

`\bar x=90\ min`

`z=(90-80)/(10)\\ z=1`

From the probability distribution tables (Cumulative Standardized normal distribution table)

Probability is P(z<1)=0.8413

Number of students=0.8413*60

Number of students to complete the exam=50.478≅50

Number of students unable to complete the exam=60-50=10 students

Answer 2

A) P=2.28%

B) P=28.57%

C) I expect 10 students to be unable to complete the exam in the alloted time.

Explanation:

In order to solve this problem, we will need to find the respective z-scores. The z-scores are found by using the following formula:

`z=(x-\mu)/(sigma)`

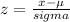
Where:

z= z-score

x= the value to normalize

`\mu = mean`

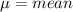
`\sigma`= standard deviation

The z-score will help us find the area below the normal distribution curve, so in order to solve this problem we need to shade the area we need to find. (See attached picture)

A) First, we find the z-score for 60 minutes, so we get:

`z=(60-80)/(10)=-2`

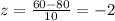
So now we look for the z-score on our normal distribution table. Be careful with the table you are using since some tables will find areas other than the area between the mean and the desired data. The table I used finds the area between the mean and the value to normalize.

so:

A=0.4772 for a z-score of -2

since we want to find the number of students that take less than 60 minutes, we subtract that decimal number from 0.5, so we get:

0.5-0.4772=0.0228

therefore the probability that a student finishes the exam in less than 60 minutes is:

P=2.28%

B) For this part of the problem, we find the z-score again, but this time for a time of 75 minutes:

`z=(75-80)/(10)=-0.5`

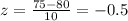
and again we look for this z-score on the table so we get:

A=0.1915 for a z-score of -0.5

Now that we got this area we subtract it from the area we found for the 60 minutes, so we get:

0.4772-0.1915=0.2857

so there is a probability of P=28.57% of chances that the students will finish the test between 60 and 75 minutes.

C) Finally we find the z-score for a time of 90 minutes, so we get:

`z=(90-80)/(10)=1`

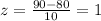
We look for this z-score on our table and we get that:

A=0.3413

since we need to find how many students will take longer than 90 minutes to finish the test, we subtract that number we just got from 0.5 so we get:

0.5-0.3413=0.1586

this means there is a 15.86% of probabilities a student will take longer than 90 minutes. Now, since we need to find how many of the 60 students will take longer than the 90 available minutes, then we need to multiply the total amount of students by the percentage we previously found, so we get:

60*0.1586=9.516

so approximately 10 Students will be unavailable to complete the exam in the allotted time.