Question

Suppose you deposit $1,250 at the end of each quarter in an account that will earn interest at an annual rate of 15 percent compounded quarterly. How much will you have at the end of four years

Answer 1

To calculate the amount of money you will have at the end of four years with quarterly deposits and compounded interest, use the formula for compound interest:

`A = P(1 + r/n)^(nt)`

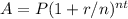
. Substituting the given values, the result is approximately $1,776.40.

Step-by-step explanation:

To calculate the amount of money you will have at the end of four years with quarterly deposits and compounded interest, you can use the formula for compound interest:

A = P(1 + r/n)^(nt)

Where:

A is the total amount of money after the specified time period

P is the principal amount (initial deposit)

r is the annual interest rate (15% in this case)

n is the number of times interest is compounded per year (4 in this case for quarterly compounding)

t is the specified time period in years (4 in this case)

Let's substitute the given values into the formula:

`A = 1250(1 + 0.15/4)^(4*4)`

`A = 1250(1 + 0.0375)^(16)`

`A = 1250(1.0375)^(16)`

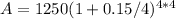
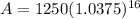
A ≈ 1250 * 1.82212

A ≈ $1,1776.4

Therefore, you will have approximately $1,776.40 at the end of four years.

Answer 2

The amount at the end of 4 years is $2,252.79.

Step-by-step explanation:

The amount formula for the compound interest compounded quarterly is:

`A=P[1+(r)/(4)]^(4t)`

Here,

A = Amount after t years

P = Principal amount

t = number of years

r = interest rate

Given:

P = $1,250, r = 0.15, t = 4 years.

The amount at the end of 4 years is:

`A=P[1+(r)/(4)]^(4t)\\=1250*[1+(0.15)/(4)]^(4*4)\\=1250*1.80223\\=2252.7875\\\approx2252.79`

Thus, the amount at the end of 4 years is $2,252.79.