Question

An empty glass soda bottle is to be use as a musical instrument. In order to be tuned properly, the fundamental frequency of the bottle be 440.0 Hz.

(a) If the bottle is 25.0 cm tall, how high should it be filled with water to produce the desired frequency?
(b) What is the frequency of the nest higher harmonic of this bottle?

Answer 1

(a). The bottle filled at the height is 5.5 cm

(b). The frequency of the nest higher harmonic of this bottle is 880 Hz.

Step-by-step explanation:

Given that,

Frequency = 440.0 Hz

Height of bottle = 25.0 cm

Suppose,

Let the bottle be filled to height h.

For a pipe with one end open,

We need to calculate the length of the pipe

Using formula of fundamental frequency

`F=(v)/(4L)`

`L=(v)/(4f)`

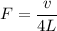
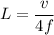
Where, L = length

v = speed of sound

Put the value into the formula

`L=(343)/(4*440)`

`L=0.195\ m`

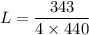
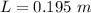
(a). We need to calculate the height

Using formula of height

`h=H-l`

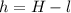
Where, H = height of bottle

l = length of pipe

Put the value into the formula

`h=25.0*10^(-2)-0.195`

`h=0.055\ m`

`h=5.5\ cm`

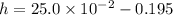
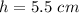
(b). We need to calculate the frequency of the nest higher harmonic of this bottle

Using formula of frequency

`f_(next)=nf_(1)`

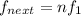
Where,
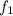`f_(1)`=fundamental frequency

Put the value into the formula

`f_(2)=2*440`

`f_(2)=880\ Hz`

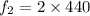
Hence, (a). The bottle filled at the height is 5.5 cm

(b). The frequency of the nest higher harmonic of this bottle is 880 Hz.

Answer 2

Step-by-step explanation:

For a pipe with one end open ,we have the formula for fundamental frequency as

`f_1= (v)/(4L)`

v= velocity of sound in air =340 m/s

L= length of pipe

hence,
`L= (v)/(4f_1)`

given f_1 = 440 Hz

Substituting , L = 340/(4×440) = 0.193 m

a) Let the bottle be filled to height , h.

Given that height of bottle ,H = 25 cm = 0.25 m

Also we found out that length of pipe L = 0.193 m

So, we have h = H - L

= 0.25 - 0.193 = 0.057 m = 5.7 cm.