Question

anna litical is practicing a centripetal force demonstration at home. she fills a bucket with water, ties it to a strong rope, and spins it in a circle. Anna spins the bucket when its half- full of water and when it is quater- full of water. In which case is more force required to stop spin the bucket circle.

Answer 1

Answer: so there is potiental enrgy need to stop spinning the bucket

Explanation:The Force of and bucket outcome is determed by the force of that i uesd to

Answer 2

half filled bucket requires more force to stop

Step-by-step explanation:

When spinning a bucket half filled it is clear that is has greater mass of water than the quarter filled bucket.

While revolving any mass tied about a fixed point we have a centripetal force acting on the bucket which makes it take the circular path during the motion.

This is centripetal force is given as:

`F_c=m.(v^2)/(r)`

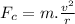
where:

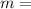`m=` mass of the revolving body

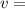`v=` tangential velocity

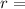`r=` radius of revolution

• From the above equation we observe that centripetal force is directly proportional to mass and square of the velocity but inversely proportional to the radius of the revolution which is same as the length of the rope between the hand and the bucket (more precisely the distance between the center of revolution and the center of mass of the revolving body). While this force acts inward to the circular path and not along the tangential direction.

The revolving mass has to be brought to rest in this case the momentum of the heavier mass will be greater and from the Newton's second law of motion we have the the rate of change in momentum directly proportional to the force applied.

Mathematically:

`F=(d)/(dt)(m.v)`

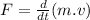
here the mass is constant so,

`F=m.(d)/(dt) v`

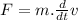
Therefore if the length of the rope, and the speed of revolution is same in both the case then the half filled bucket whose mass is greater than the quarter filled bucket will require more force to stop the circular motion of the bucket.