Question

Identify the triangle that contains an acute angle for which the sine and cosine ratios are equal. 1. Triangle A B C has angle measures 50 degrees, 40 degrees, and 90 degrees. 2. Triangle A B C has angle measures 45 degrees, 45 degrees, 90 degrees. 3. The lengths of sides A C and C B are congruent. 4. Triangle A B C has angle measures 68 degrees, 22 degrees, and 90 degrees. 5. Triangle A B C has angle measures 60 degrees, 30 degrees, and 90 degrees.

Answer 1

IT'S the second option

Explanation:

Answer 2

The correct option: (2) Triangle ABC that has angle measures 45°, 45° and 90°.

Explanation:

It is provided that a triangle ABC has an acute angle for which the sine and cosine ratios are equal to 1.

Let the acute angle be m∠A.

For the sine and cosine ratio of m∠A to be equal to 1, the value of Sine of m∠A should be same as value of Cosine of m∠A.

The above predicament is possible for only one acute angle, i.e. 45°, since the value of Sin 45° and Cos 45° is,

`Sin\ 45^(o) =Cos\ 45^(o) = (1)/(√(2) )`

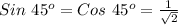
So for acute angle 45° the ratio of Sin 45° and Cos 45° is:

`(Sin\ 45^(o))/(Cos\ 45^(o)) = ((1)/(√(2) ) )/((1)/(√(2) ) ) = 1`

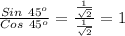
Hence one of the angles of a triangle is, m∠A = 45°.

Comparing with the options provided the triangle is,

Triangle ABC that has angle measures 45°, 45° and 90°.

Thus, the provided triangle is a right angled isosceles triangle, since it has two similar angles.