Question

In the figure above, square ABCD and triangle EFG have the same areas. If AB =6 and EG =8, what is the height o triangle EFG?

Answer 1

The height of triangle EFG is 9 units

Explanation:

see the attached figure to better understand the problem

step 1

Find the area of a square ABCD

The area of a square is equal to

`A=b^2`

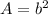
where

b is the length side of the square

we have

`b=AB=6\ units`

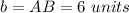
substitute

`A=6^2=36\ units^2`

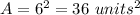
step 2

Find the height of triangle EFG

The area of triangle EFG is equal to

`A=(1)/(2)(b)(h)`

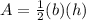
where

b is the base of triangle

h is the height of triangle

we have

`b=EG=8\ units`

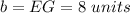
`A=36\ units^2` ---> area of triangle EFG is the same that the area of square ABCD

substitute the given values in the formula

`36=(1)/(2)(8)(h)`

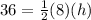
solve for h

`36=4h\\h=9\ units`

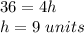
therefore

The height of triangle EFG is 9 units