Question

A new, previously unknown, planet Vulcan was discovered in our solar system. We measure an orbital period of 103 Earth days for the new planet. We send some astronauts to travel to the planet and they measure the planet's gravitational acceleration to be 8.2 m/s2 on its surface. They also determine that the planet's radius is half the radius of Earth.

Q1. How far away from the sun is the new planet?

(A) 8.3 x 100 m
(B) 6.4 x 100 m
(C) 1.7 x 100 m
(D) 9.5 x 1010 m
(E) 2.3 x 1010 m

Q2. What is the mass of planet Vulcan?

(A) 1.3 x 1024 kg
(B) 5.4 x 1024 kg
(C) 9.8 x 1024 kg
(D) 0.2 x 102 kg
(E) 4.8 x 1024 kg


Q3. The astronauts also discover a moon that orbits planet Vulcan with a period of 63 days. How far away is the moon from the planet Vulcan?

(A) 1 x 108 m
(B) 20 x 108 m
(C) 460 x 108 m
(D) 9 x108 m
(E) 4 x 10 m

Q4. The astronauts visit the newly discovered moon to study it. They measure the gravitational acceleration on the surface of the moon to be 2.7 m/s. When their mission is finished, they try to escape from the moon. They measure that the minimum velocity to escape the moon is 3,000 m/s. What is the mass of the moon?

(A) 1.1 x 1023 kg
(B) 5.0 x 1023 kg
(C) 7.8 x 1023 kg
(D) 29 x 104 kg
(E) 370 x 1023 kg

Answer 1

Q1. corect is B, Q2. it is A, Q3. E and Q4. A

Step-by-step explanation:

Q1 For this exercise we can use Newton's second law where acceleration is centripetal.

F = m a

a = v² / r.

G m M / r² = m v² / r

G M / r = v²

The velocity has a constant magnitude whereby we can divide the length of the circular orbit (2π r) between the period

G M / r = (2π r / T)²

r³ = G M T2 / 4π²

Let's calculate

T = 103 day (24 h / 1 day) (3600 s / 1h) = 8,899 10⁶ s

r³ = 6.67 10⁻¹¹ 1.99 10³⁰ (8,899 10⁶) 2 / 4π²

r = ∛ (266.25 10³⁰)

r = 6.4 10¹⁰ m

The distance matches the value in part B

Q2 Astronauts have measured the acceleration of gravity, so we can use the second law with a body on the planet's surface

F = m g

G m M_p / R_p² = m g

G M_p / R_p² = g

M_p = g R_p² / G

They indicate that the radius of the planet is half the radius of the Earth

R_p = ½ R_earth

R_p = ½ 6.37 10⁶

R_p = 3.185 10⁶ m

Let's calculate

M_p = 8.2 (3,185 10⁶)² / 6.67 10⁻¹¹

M_p = 1.25 10²⁴ kg

The correct answer is A

Q3 We use Newton's second law again, with part Q1, where M is the mass of the planet and m is the mass of the moon

r³ = G M T² / 4π²

T = 63 days (24h / 1day) (3600s / 1h) = 5.443 10⁶ s

r³ = 6.67 10⁻¹¹ 1.25 10²⁴ (5.443 10⁶)² / 4π²

r = ∛ (62.56807 10²⁴)

r = 3.97 10⁸ m

The correct answer is E

Q4 To calculate this part let's use the conservation of mechanical energy,

Starting point The surface of the moon

Em₀ = K + U = ½ m v2 - G m M / r

Final point. Infinity with zero speed

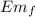`Em_(f)` = 0

Em₀ = Em_{f}

½ m v² - G m M / R = 0

v² = 2 G M / r

M = v2 r / 2G

r = 2 G M / v²

Since we don't know the radius of the moon, we will also use the equation in part 2

M = g r² / G

r = √ GM / g

Let's replace

2G M / v² = √ G M / g

4 G M / v⁴ = 1 / g

M = v⁴ / (g 4G)

M = 3000⁴ / (2.7 4 6.67 10-11)

M = 1.12 10²³ kg

corract is A