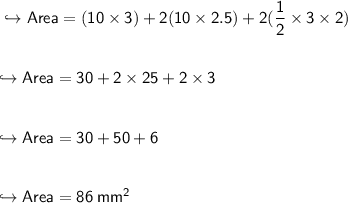❍ Concept :-
We can solve these questions by using the formulas of area of triangle and rectangle, which will make our work easier. So, we know that,
⠀
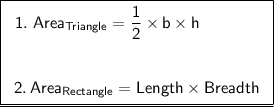
Using these formulas and figuring out the number of triangles and rectangles in each shape, we will solve this question.
⠀
✰ Solution :-
⠀
1. In this square pyramid, if we closely observe, we will get to know that there are 1 rectangle and 4 triangular faces. Thus,
⠀

⠀
2. Now, here, we can use the formula of total surface area for cuboid, i.e.
⠀
TSA = 2( lb + bh + hl )
⠀

⠀
Extra Credit Question.
⠀
Here, we can find out the total surface area by finding,
⠀
Base area i.e. length x breadth ( B.A. )
Side area i.e. length x breadth ( S.A. )
triangular area = 1/2 x b x h ( T.A. )
⠀
Now,
⠀
TSA = BA + 2 x S.A. + 2 x T.A.
⠀