Question

A resultant vector is 8.00 units long and makes an angle of 43.0 degrees measured ������� – ��������� with respect to the positive � − ����. What are the magnitude and angle (measured ������� – ��������� with respect to the positive � − ����) of the equilibrant vector? Please show all steps in your calculations

Answer 1

223 degree

Step-by-step explanation:

We are given that

Magnitude of resultant vector= 8 units

Resultant vector makes an angle with positive -x in counter clockwise direction

`\theta=43^(\circ)`

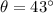
We have to find the magnitude and angle of the equilibrium vector.

We know that equilibrium vector is equal in magnitude and in opposite direction to the given vector.

Therefore, magnitude of equilibrium vector=8 units

x-component of a vector=
`v_x=vcos\theta`

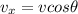
Where v=Magnitude of vector

Using the formula

x-component of resultant vector=
`v_x=8cos43=5.85`

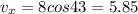
y-component of resultant vector=
`v_y=vsin\theta=8sin43=5.46`

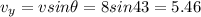
x-component of equilibrium vector=
`v_x=-5.85`

y-component of equilibrium vector=
`-v_y=-5.46`

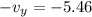
Because equilibrium vector lies in III quadrant

`\theta=tan^(-1)((v_x)/(v_y))=tan^(-1)((-5.46)/(-5.85))=43^(\circ)`

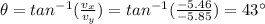
The angle
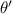`\theta'`lies in III quadrant

In III quadrant ,angle =
`\theta'+180^(\circ)`

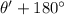
Angle of equilibrium vector measured from positive x in counter clock wise direction=180+43=223 degree