Question

Tristan and Iseult play a game where they roll a pair of dice alternatingly until Tristan wins by rolling a sum 9 or Iseult wins by rolling a sum of 6.

If Tristan rolled the dice first, what is the probability that Tristan wins?

Answer 1

If Tristan rolled the dice first the probability that Tristan wins is 0.474.

Explanation:

The probability of an event E is computed using the formula:

`P(E)=(Favorable\ otucomes)/(Total\ outcomes)`

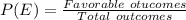
Given:

Tristan and Iseult play a game where they roll a pair of dice alternatively until Tristan wins by rolling a sum 9 or Iseult wins by rolling a sum of 6.

The sample space of rolling a pair of dice consists of a total of 36 outcomes.

The favorable outcomes for Tristan winning is:

S (Tristan) = {(3, 6), (4, 5), (5, 4) and (6, 3)} = 4 outcomes

The favorable outcomes for Iseult winning is:

S (Iseult) = {(1, 5), (2, 4), (3, 3), (4, 2) and (5, 1)} = 5 outcomes

Compute the probability that Tristan wins as follows:

`P(E)=(Favorable\ otucomes)/(Total\ outcomes)\\ P(Tristan\ wins)=(4)/(36)\\P(T)=(1)/(9) \\\approx0.1111`

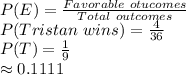
Compute the probability that Iseult wins as follows:

`P(E)=(Favorable\ otucomes)/(Total\ outcomes)\\ P(Iseult\ wins)=(4)/(36)\\P(I)=(1)/(9) \\\approx0.1111`

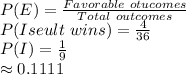
If Tristan plays first, then the probability that Tristan wins is:

= P(T) + P(T')P(I')P(T) + P(T')P(I')P(T')P(I')P(T)+...

=P(T) + [(1-P(T))(1-P(I))P(T)]+[(1-P(T))(1-P(I))(1-P(T))(1-P(I))P(T)]+...

`=0.1111+(0.8889*0.8611*0.1111)+(0.8889*0.8611*0.8889*0.8611*0.1111))+...\\=0.1111[1+(0.8889*0.8611)+(0.8889*0.8611)^(2)+...]\\`This is an infinite geometric series.

The first term is, a = 0.1111 and the common ratio is, r = (0.8889×0.8611).

The sum of infinite geometric series is:

`S_(\infty)=(a)/(1-r)\\ =(0.1111)/(1-(0.8889*0.8611)\\ =0.47364\\\approx0.474`

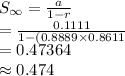
Thus, the probability that Tristan wins if he rolled the die first is 0.474.