Question

The computers of nine engineers at a certain company are to be replaced. Four of the engineers have selected laptops and the other 5 have selected desktops. Suppose that four computers are randomly selected.

(a) How many different ways are there to select four of the eight computers to be set up?
(b) What is the probability that exactly three of the selected computers are desktops?
(c) What is the probability that at least three desktops are selected?

Answer 1

(a) There are 70 different ways set up 4 computers out of 8.

(b) The probability that exactly three of the selected computers are desktops is 0.305.

(c) The probability that at least three of the selected computers are desktops is 0.401.

Explanation:

Of the 9 new computers 4 are laptops and 5 are desktop.

Let X = a laptop is selected and Y = a desktop is selected.

The probability of selecting a laptop is =
`P(Laptop) = p_(X) = (4)/(9)`

The probability of selecting a desktop is =
`P(Desktop) = p_(Y) = (5)/(9)`

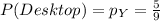
Then both X and Y follows Binomial distribution.

`X\sim Bin(9, (4)/(9))\\ Y\sim Bin(9, (5)/(9))`

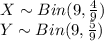
The probability function of a binomial distribution is:

`P(U=k)={n\choose k}*(p)^(k)* (1-p)^(n-k)`

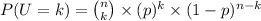
(a)

Combination is used to determine the number of ways to select k objects from n distinct objects without replacement.

It is denotes as:
`{n\choose k}=(n!)/(k!(n-k)!)`

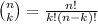
In this case 4 computers are to selected of 8 to be set up. Since there cannot be replacement, i.e. we cannot set up one computer twice or thrice, use combinations to determine the number of ways to set up 4 computers of 8.

The number of ways to set up 4 computers of 8 is:

`{8\choose 4}=(8!)/(4!(8-4)!)\\=(8!)/(4!* 4!) \\=70`

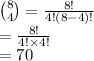
Thus, there are 70 different ways set up 4 computers out of 8.

(b)

It is provided that 4 computers are randomly selected.

Compute the probability that exactly 3 of the 4 computers selected are desktops as follows:

`P(Y=3)={4\choose 3}*((5)/(9))^(3)* (1-(5)/(9))^(4-3)\\=4*(125)/(729)*(4)/(9)\\ =0.304832\\\approx0.305`

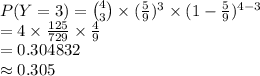
Thus, the probability that exactly three of the selected computers are desktops is 0.305.

(c)

Compute the probability that of the 4 computers selected at least 3 are desktops as follows:

`P(Y\geq 3)=1-P(Y<3)\\=1-[P(Y=0)+P(Y=1)+P(Y=2)]\\=1-[({4\choose 0}*((5)/(9) )^(0)* (1-(5)/(9) )^(4-0)+({4\choose 1}*((5)/(9) )^(1)* (1-(5)/(9) )^(4-1)+({4\choose 2}*((5)/(9) )^(2)* (1-(5)/(9) )^(4-2)]\\=1-0.59918\\=0.40082\\\approx0.401`

Thus, the probability that at least three of the selected computers are desktops is 0.401.