Answer:
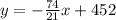
Explanation:
Given:
The level of a lake is falling linearly.
On Jan 1, the level is 452 inches
On Jan 21, the level is 378 inches.
Now, a linear function can be represented in the form:

Where, 'm' is the rate of change and 'b' is initial level
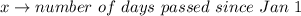
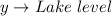
So, let Jan 1 corresponds to the initial level and thus b = 452 in
Now, the rate of change is given as the ratio of the change in level of lake to the number of days passed.
So, from Jan 1 to Jan 21, the days passed is 21.
Change in level = Level on Jan 21 - Level on Jan 1
Change in level = 378 in - 452 in = -74 in
Now, rate of change is given as:
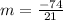
Hence, the function to represent the lake level is
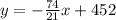
Where, 'x' is the number of days passed since Jan 1.