Answer:
The question is incomplete, below is the complete question,
"A water balloon is launched at a speed of (15.0+A) m/s and an angle of 36 degrees above the horizontal. The water balloon hits a tall building located (18.0+B) m from the launch pad. At what height above the ground level will the water balloon hit the building? Calculate the answer in meters (m) and rounded to three significant figures. A=12, B=2"
Answe:
12.1m
Step-by-step explanation:
Below are the data given
Speed, V=(15+A) = 15+12=27m/s
Angle of projection, ∝=36 degree
Distance from building = 18+B=18+2=20m
Since the motion describe by the object is a projectile motion, and recall that in projectile motion, motion along the horizontal path has zero acceleration and motion along the vertical path is under gravity,
the Velocity along the horizontal path is define as
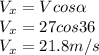
the velocity along the Vertical path is

Since the horizontal distance from the point of projection to the building is 20m, we determine the time it takes to cover this distance using the simple equation of motion
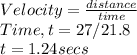
The distance traveled along the vertical axis is given as
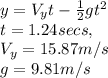
if we substitute values, we arrive at
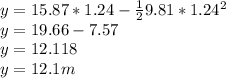
Hence the water balloon hit the building at an height of 12.1m