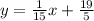Question

Write an equation in slope-intercept form of the line perpendicular to y = - 1 5 x + 1 4 that passes through the point (3, 4).

Answer 1

The equation of the line is
`y=(1)/(15) x+(19)/(5)`

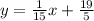
Step-by-step explanation:

The equation is
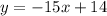`y=-15x+14` and passes through the point (3,4)

To find the equation of the line in slope intercept form, first we shall find the slope.

This equation is of the slope-intercept form
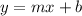`y=m x+b`, we shall find the value of slope.

Thus, slope m = -15

Since, the line is perpendicular, the negative slope is given by
`(-1)/(m)`

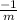
Thus, the new slope is
`m=(1)/(15)`

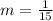
Now, we shall find the equation of the line perpendicular to the slope
`(1)/(15)` is

`y-y_(1)=(1)/(15) \left(x-x_(1)\right)`

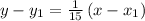
Let us substitute the points (3,4), we have,

`y-4=(1)/(15) \left(x-3\right)`

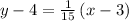
Muliplying the term within the bracket, we get,

`y-4=(1)/(15)x-(1)/(5)`

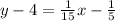
Adding both sides of the equation by 4, we get,

`y=(1)/(15)x-(1)/(5)+4`

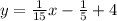
Adding the like terms, we have,

`y=(1)/(15) x+(19)/(5)`

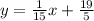
Thus, the equation in slope intercept form of the line is
`y=(1)/(15) x+(19)/(5)`