2 Answers

David Driscoll · Answer 1 · 2021-09-28T07:02:56+0000

The required "option A)
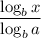$(\log_(b)x)/(\log_(b)a)$ " is correct.

Explanation:

We have,

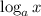
$\log _(a)x$

To find, the value of
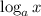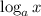$\log _(a)x$ = ?

∴
$\log _(a)x$ , where a, b and x are positive

a ≠ 1 and b ≠ 1

We know that,

The logarithm identity,

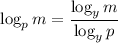
$\log_(p)m=(\log_(y)m)/(\log_(y)p)$

∴
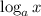$\log _(a)x$ =
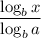
$(\log_(b)x)/(\log_(b)a)$

Where, b is the common base of logarithm

∴ The value of
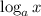$\log _(a)x$ =
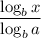
$(\log_(b)x)/(\log_(b)a)$

Thus, the required option A)
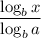$(\log_(b)x)/(\log_(b)a)$ is correct.