GF = 11, GE = 28, HF = 14,

Solution:
Given data:
DE = 11, GH = 14
In rectangle, opposite sides are equal.
DE = GF
GF = 11
Property of a rectangle:
The diagonals of a rectangle are equal in length and they bisect each other.
Half of diagonal GE = GH = 14
GE = 2 × GH
= 2 × 14
GE = 28
HF is also a half of the diagonal DF.
By property of a rectangle, GH = HF
HF = 14
Diagonal of a rectangle formula:
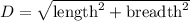

Squaring on both sides, we get
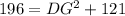

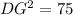
Taking square root on both sides, we get

Hence GF = 11, GE = 28, HF = 14,
 .
.