Question

falls freely from rest and strikes the ground. During the collision with the ground, he comes to rest in a time of 0.040 s. The average force exerted on him by the ground is 18 000 N, where the upward direction is taken to be the positive direction. From what height did the student fall

Answer 1

y = 2,645 10⁴ / m²

m=80 kg, y = 4.13 m

Step-by-step explanation:

We must solve this problem in two parts, one when it is in free fall and another for the collision with the floor

Let's start by analyzing the crash with the floor,

Initial instant When it arrives but if you start to stop

p₀ = m v

Final moment. When he stopped

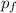`p_(f)` = 0

The momentum is related to the moment by

I = Δp = p_{f} –p₀

F t = 0 - mv

v = -F t / m

Let's calculate

v = -18000 0.040 / m

v = -720 / m

The sign indicates that the speed goes down

Now we use energy conservation at two points

Lowest point. Just before crashing

Em₀ = K = ½ m v²

Highest point. From where it began to fall

Em_{f} = U = m g y

Energy is conserved in the fall

Em₀ = Em_{f}

½ m v² = m g y

y = ½ v² / g

y = ½ (720 / m)² /9.8

y = 2,645 10⁴ / m²

For an explicit height value, the object's mass must be known, suppose the masses are m = 80 kg

y = 2,645 10⁴/80²

y = 4.13 m