Question

If our eyes could see a slightly wider region of the electromagnetic spectrum, we would see a fifth line in the Balmer series emission spectrum. Calculate the wavelength λλlambda associated with the fifth line.

Answer 1

λ = 397 nm

Step-by-step explanation:

given,

Rydberg wavelength equation for Balmer series

`(1)/(\lambda)=R((1)/(n_f^2)-(1)/(n_i^2))`

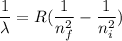
R is the Rydberg constant, R = 1.097 x 10⁷ m⁻¹

n_i = initial energy level

n_f = final energy level

where as for Balmer series n_f = 2

n_i = 7

`(1)/(\lambda)=(1.097* 10^7)((1)/(2^2)-(1)/(7^2))`

`(1)/(\lambda)=(1.097* 10^7)((1)/(2^2)-(1)/(7^2))`

`(1)/(\lambda)=2.5186* 10^6`

`\lambda = 3.97* 10^(-7)`

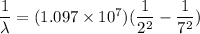
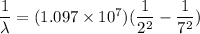
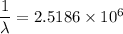
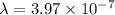
Hence, the wavelength is equal to λ = 397 nm