Question

A dog running in an open field has components of velocity vx = 2.6 m/s and vy = -1.8 m/s at t1 = 10.0 s. For the time interval from t1 = 10.0 s to t2 = 20.0 s, the average acceleration of the dog has magnitude 0.45 m/s2 and direction 31.0o measured from the + x-axis toward the + y-axis. At t2 = 20.0 s, (a) what are the x- and y-components of the dog’s velocity? (b) What are the magnitude and direction of the dog’s velocity? (c) Sketch the velocity vectors at t1 and t2. How do these two vectors differ?

Answer 1

a) vₓ = 6,457 m / s , v_{y} = 0.518 m / s , b) v = 6.478 m / s, θ = 4.9°

Step-by-step explanation:

a) This is a kinematic problem, let's use trigonometry to find the components of acceleration

sin 31 =
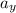`a_(y)` / a

cos 31 = aₓ = a

a_{y} = a sin31

aₓ = a cos 31

Now let's use the kinematic equation for each axis

X axis

vₓ = v₀ₓ + aₓ (t-t₀)

vₓ = v₀ₓ + a cos 31 (t-t₀)

vₓ = 2.6 + 0.45 cos 31 (20-10)

vₓ = 6,457 m / s

Y Axis

v_{y} = v_{oy} + a_{y} t

v_{y} = v_{oy} + a_{y} sin31 (t-to)

v_{y} = -1.8 + 0.45 sin31 (20-10)

v_{y} = 0.518 m / s

b) let's use Pythagoras' theorem to find the magnitude of velocity

v = √ (vₓ² + v_{y}²)

v = √ (6,457² + 0.518²)

v = √ (41.96)

v = 6.478 m / s

We use trigonometry for direction

tan θ = v_{y} / vₓ

θ = tan⁻¹ v_{y} / vₓ

θ = tan⁻¹ 0.518 / 6.457

θ = 4.9°

c) let's look for the vector at the initial time

v₁ = √ (2.6² + 1.8²)

v₁ = 3.16 m / s

θ₁ = tan⁻¹ (-1.8 / 2.6)

θ₁ = -34.7

We see that the two vectors differ in module and direction, and that the acceleration vector is responsible for this change.

a = (v₂ -v₁) / (t₂-t₁)